1. 삽입 정렬 시간복잡도 : O(n²)
template <class T>
void Insert(const T& e, T *a, int i)
{// e를 정렬된 리스트 a[1:i]에 삽입하여 결과
// 리스트 a[1: i+1]도 정렬되게 한다.
// 배열 a는 적어도 i+2 원소를 포함할 공간을 가지고 있어야 한다.
// a[0] = -∞; 가 저장되어 있음.
while(e <a[i])
{
a[i+1] = a[i];
i--;
}
a[i+1] = e;
}
Template <class T>
void InsertionSort(T *a, const int n) // a[1:n]을 오름차순으로 정렬
{
for(int j=2; j<=n; j++) {
T temp = a[j];
insert(temp, a, j-1); // a[j]가 삽입 원소이다.
}
}
2. 퀵 정렬 시간복잡도 : O(logn)
pivot(중추값)을 이용하여 정렬하는 정렬 알고리즘. left 값은 중추값 보다 작아야되고, right 값은 커야된다.
그 결과 중추값보다 작은 원소들은 중추값 왼쪽으로, 큰 원소들은 중추값보다 큰 쪽으로 옮겨진다.

위의 퀵 정렬은 가장 좌측값을 pivot으로 삼는 퀵 정렬이다.
첫 재귀에 대한 설명,
0. 재귀함수이므로 받은 매개변수로 종료 조건문인 if(left>right)가 존재한다.
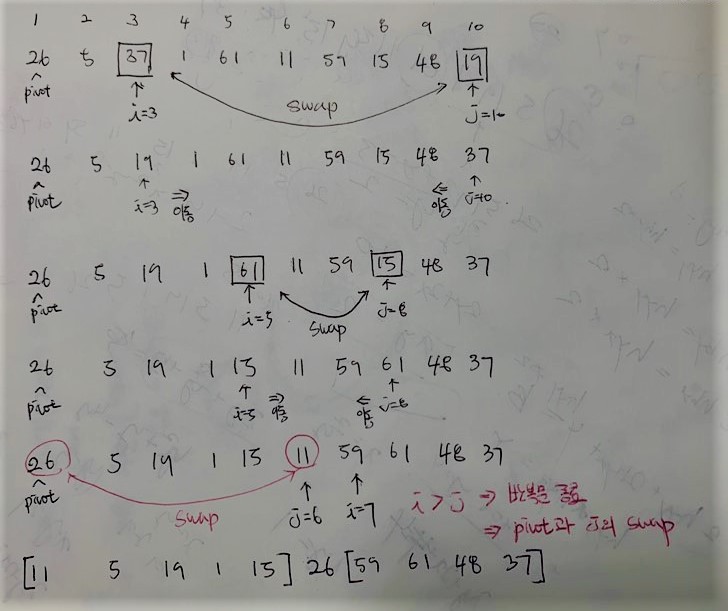
1. Pivot: 26. i=1부터 우측으로 이동하며 pivot보다 큰 값을 찾고, j는 10부터 좌측으로 이동하며 pivot보다 작은 값을 찾는다.
2. 위의 결과로 i=3[37], j=10[19]가 선택되고, i<j이므로 둘을 스왑한다.
3. 다시 계속해서 진행한다. i=5[61], j=8[15]가 선택되고 i<j이므로 둘을 스왑한다.
4. 다시 계속해서 진행한다. i=7[59], j=6[11]이 선택되지만 i>j이므로 while문이 끝난다. 이때, j가 가리키는 값과 pivot값의 위치를 바꾸게 된다.
5. 이후 pivot을 중심으로 양 옆에 대해 다시 재귀적으로 퀵 정렬한다.
void quickStort(int[] arr, int left, int right){
if(left < right){
int i = left+1;
int j = right;
int pivot = arr[(left+right)/2];
while(i<j){
while(arr[j]>pivot) j--;
while(i<j && arr[i]< pivot) i++;
swap(arr,i,j);
}
quickStort(arr, left, i-1);
quickStort(arr, i+1, right);
}
}
3. 합병 정렬 시간복잡도 : O(nlogn)
이미 정렬된 2개의 리스트를 1개의 정렬된 리스트로 만드는 과정을 반복한다.
기존 정렬에 비해 두배의 메모리 공간이 필요하다.

void merge(int[] arr, int left, int mid, int right){
int i = left;
int j = mid+1;
int k = left;
//두 범위로 나누어 빈 배열에 비교하며 추가
while(i<=mid && j<=right){
if(arr[i]>arr[j])
tempArr[k++]=arr[j++];
else
tempArr[k++]=arr[i++];
}
//남은 범위가 있을 경우 추가
if(i>mid){
for(int x=j;x<=right;x++)
tempArr[k++] = arr[x];
}else{
for(int x=i;x<=mid;x++)
tempArr[k++] = arr[x];
}
//복사
for(int x=left; x<=right; x++)
arr[x]=tempArr[x];
}void mergeSort(int[] arr, int left, int right){
if(left<right){
int mid = (left+right)/2;
mergeSort(arr, left, mid);
mergeSort(arr, mid+1, right);
merge(arr,left,mid,right);
}
}void main(){
int i;
int n = SIZE;
int list[n] = {21, 15, 12, 23, 25, 7, 10, 22};
merge_sort(list, 0, n-1);
for(i=0; i<n; i++){
printf("%d\n", list[i]);
}
}참고: gmlwjd9405.github.io/2018/05/08/algorithm-merge-sort.html
4. 히프 정렬 시간복잡도 : O(nlogn)
방법 1. 배열을 히프로 조정 후 히프 트리 자체를 정렬
배열을 히프 구조로 조정한 뒤. 루트와 맨 마지막 값을 교체한 뒤. 마지막 값인 최대 값을 제외하고 조정 작업을 반복하여 정렬하게 된다.
/*조정 함수*/
void Adjust(int *a, const int r, const int n)
// r 을 루트 노드로 하는 이진 트리를 히프 성질을 만족하도록 조정한다
// r 의 왼쪽과 오른쪽 서브트리는 히프 성질을 이미 만족한다
// 어떤 노드도 n보다 큰 인덱스를 갖지 않는다
{
int e = a[r] ;
for(int j = 2 * r; j <= n; j *= 2) //j=2*r --> 루트 노드의 왼쪽 자식
{
if(j < n && a[j] < a[j+1]) j++ ; //우측 자식이 있다면 비교하여 우측이 클 경우 j증가
if(e >= a[j]) break; //루트가 크다면 종료
else//루트가 작다면
a[j/2] = a[j]; //자식을 위로 올림
}
a[j/2] = e; //기존 루트였던 값을 최종 위치에 삽입
}
/*히프 정렬 함수*/
void HeapSort(int *a, const int n)
// a[1:n]을 오름차순으로 정렬한다.
{
for(int i = n/2; i >= 1; i--) // 히프로 변환 i=n/2인 이유. 리프 노드는 더 이상 내릴 곳 없음
Adjust(a, i, n);
//실제 정렬 과정 시작
for(i=n-1; i >= 1; i--)
{
swap(a[1],a[1+1]); //가장 값이 큰 루트 노드를 리프노드 마지막으로 이동.
Adjust(a, 1, i); // 이동된 마지막 노드를 제외하고 트리를 재조정
}
}
방법2. 히프 트리를 새로 생성하고, 배열의 값을 히프에 추가한 뒤 모두 제거하여 구현.
이 방법은 히프를 생성하기 때문에 공간복잡도가 조금 더 크다.
void heapSort(int[] arr, int size){
Heap heap = new Heap(size+1);
for(int i=0; i<size;i++){
heap.add(arr[i]);
}
for(int i=0; i<size;i++){
arr[i]=heap.pop();
}
}'Domain > 자료구조' 카테고리의 다른 글
| 4. 히프 트리(Heap Tree) (0) | 2020.03.12 |
|---|---|
| 5. 이진 탐색 트리(BST, Binary Searching Tree) (0) | 2020.03.12 |
| 6. 그래프 (0) | 2020.03.12 |
| 7. 탐색 (0) | 2020.03.11 |
| 9. Hashing(해싱) (0) | 2020.03.11 |


