1. 그래프 표현법 - 무방향, 비가중치
인접행렬 희소그래프가 아닌 경우에 주로 사용된다. (희소 그래프일 경우 탐색에 불필요한 자원이 낭비된다.) 정점이 서로 연결된 경우 1로 표시하고 그렇지 않은 경우 0으로 표시한다.
장점으로는 구현이 간단하고 연결을 확인하는데에 O(1)의 시간복잡도만 필요하다. (1과 2의 연결확인은 length[1][2]의 값을 확인하면 됨.) 단점으로는 특정 노드에 연결된 모든 노드 n개를 방문하기 위해서 O(n)의 시간 복잡도가 필요하다. 그렇기에 위에서 말한 희소그래프가 아닌 경우에 주로 사용된다. 예를들어 노드가 1억개이고 간선이 두개 뿐인 희소그래프를 고려해보면, 특정 노드에 연결된 노드가 무엇인지 찾기 위해 1억번의 탐색이 필요하다.
class Graph{
private:
int **length; //배열을 위한 이차원 배열
int *dist; //다익스트라
int *path; //다익스트라
bool *s; //방문을 확인
int n; //정점 수
public:
Graph(int n){
this->n = n;
length = new int*[n];
dist = new int[n]; path= new int[n]; s=new bool[n];
for(int i=0; i<n; i++){
length[i]=new int[];
for(int j=0; j<n; j++){
if(i==j)
length[i][j]=0;
else
length[i][j]=INF;
}
}
}
};인접리스트 희소 그래프일 경우에 주로 사용한다.


class ListGraph;
class Node{
friend ListGraph;
private:
int point;
Node *link;
public:
Node(int p, Node* l){
point = p; link =l;
}
};
class ListGraph{
private:
Node ** headPointer;
int n;
bool *visited;
public:
ListGraph(int size){
n = size;
headPointer = new Node*[n];
visited = new bool[n];
for(int i=0; i<n; i++){
headPointer[i]=0;
visited[i]=false;
}
}
void insertEdge(int u, int v){
Node *newNode = new Node(v,headPointer[u]);
headPointer[u]=newNode;
newNode = new Node(u,headPointer[v]);
headPointer[v]=newNode;
}
};다익스트라 알고리즘 - 방향 가중치 그래프에 적용
경로 별로 비용이 다른 가중치 그래프에서 사용하는 최단 경로를 구하는 알고리즘이다. 한 정점에서 다른 모든 정점들 까지의 최단 경로를 구한다.
과정
- 출발점 v를 포함하여 알고리즘을 통해 최단 경로가 밝혀진 정점들의 집합을 s라고 한다.
- s에 속하지 않은 정점 중 dist(거리) 값이 가장 작은 정점 u를 선택하여 집합 s에 포함시킨다. (여기서 dist는 출발점 v에서 각 정점까지의 거리(가중치)를 의미한다.)
- s에 속하지 않은 정점들 중, 0에서 시작하여 위에서 선택된 u를 거쳐서 가는 경로(0->u->w)와 직접 가는 경로(0->w)를 비교하여 더 작은 값으로 갱신한다. 즉, dist[w] = min {dist[w], dist[u]+length[u][w]}
- s에 n-1개의 정점이 포함될 때 까지 단계 2,3을 반복한다. (즉, 초기에 시작점이 s에 포함되기 때문에 n-2번 반복)
//인접 행렬을 이용함.
void shortedPath(int v){
for(int i=0; i<n; i++){
dist[i]=length[v][i];
path[i]=v;
s[i]=false;
}
s[v]=true;
for(int i=0; i<n-2; i++){
int u=choose(n); s[u]=true; //방문하지 않은 거리가 최소인 점
for(int w=0; w<n; j++){
if(!s[w]){
if(dist[w]>(dist[u]+length[u][w])){
dist[w]=dist[u]+length[u][w];
path[w]=u; //최단 비용으로 가는 경로를 탐색하기 위함.
}
}
}
}
}
실제 순서를 따라가보자

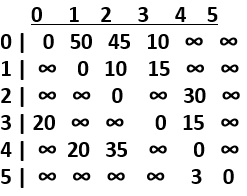
0에서 각 정점까지의 최단 비용을 구해보자.
1. 먼저 집합 s에 0을 추가한다. s={0}
2. 집합 s에 속하지 않는 정점 중 0과의 거리(비용)이 10으로 가장 작은 3을 선택한다.
3. 3을 집합 s에 추가한다. s={0,3}
4. 집합 s에 속하지 않는 정점 중, 방금 선택된 3을 거쳐서 가는 거리와의 비교를 시작한다.
- 0->1(50)과 0->3->1(10+∞), dist 배열을 그대로 유지.
- 0->2(45)와 0->3->2(10+∞), "
- 0->4(10)와 0->3->4(10+15=25), 0->4까지의 거리를 의미하는 dist[4]를 25로 초기화. (더 짧은 경로로 초기화 됨)
...
5. 위 과정을 통해 한 사이클이 끝났다. 2~4의 과정을 집합 s가 5개가 될 때까지 반복하면 된다.
(다음은 정점 4가 0과의 거리가 25로 최소이기 때문에 선택될 것이다. 그 이후 0->w와 0->4->w를 통해 경로가 갱신된다. 이후 과정은 위와 같다.)
추가로, 위 다익스트라 구현 코드에서 path배열을 통해 최단 비용으로 가는 경로를 탐색할 수 있다. 위 그래프에 다익스트라 알고리즘을 적용시킨 후의 path는 0 4 0 0 3 0이 된다. 만약, 0에서 1로의 최단 비용 경로를 알고 싶다고 가정해보자. 그럼 먼저 1번 인덱스의 값인 4, 그 다음 4번 인덱스의 값인 3, 그 다음은 3번 인덱스의 값인 0이 나온다. 이를 역순으로 나열하면 0->3->4->1이 최단 비용 경로이다. 예를 하나 더 들자면, 0에서 2로의 최단 경로를 알고 싶다면 2번 인덱스의 값인 0, 0은 출발지이기 때문에 이를 역순으로 배열하면 0->2가 최단 비용 경로이다.
2. 그래프의 탐색 (연결 그래프이며 무방향인 그래프의 경우)
하나의 정점에서 시작하여 모든 정점을 방문하는 알고리즘 (n: 정점 수, e: 간선 수)
깊이우선탐색(DFS) 시간복잡도(인접리스트) : O(e) 시간복잡도(인접행렬) : O(n²)
하나의 정점에서 시작하여 연결된 정점 중 방문이 안된 정점을 방문하는 알고리즘 (재귀적 방법으로 구현)


void DFS(int v){
cout << v<< " ";
visited[v]=true;
for(Node *i=headPointer[v]; i; i=i->link){
int x = i->point;
if(!visited[x])
DFS(x);
}
}
헤드포인터0에서 시작하여 1을 방문한뒤 재귀적 구현에 의해 헤드포인터1을 방문하고 그 다음 헤드포인터3, 그다음은 헤드포인터7, 그 다음은 헤드포인터4, 그 다음은 헤드포인터5를 방문한다. 이후 재귀가 풀려 가장 헤드포인터2를 방문하고 다시 재귀로 헤드포인터 6을 방문하게 되어 마무리 된다.
너비우선탐색(BFS) 시간복잡도(인접리스트) : O(e) 시간복잡도(인접행렬) : O(n²)
하나의 정점에서 시작하여 인접한 정점을 방문하는 알고리즘이다. 한 정점을 방문하고 그 정점과 연결된 노드들을 큐에 저장한 뒤 순서대로 방문한다.


void BFS(int x){
int v;
queue<int> Q; //#include <queue>
Q.push(x);
visited[x]=true;
while(!Q.empty()){
//큐에 값이 있을 경우 반복 -> 방문하지 않은 노드의 존재
v=Q.front();
Q.pop();
cout<<v<<' ';
for(Node *i=headPointer[v];i; i=i->link){
//인접한 노드중 방문하지 않았다면 모두 큐에 삽입.
if(!visited[i->point]){
Q.push(i->point);
visited[i->point]=true;
}
}
}
}
3. 신장 트리
연결 그래프에서 모든 정점을 포함하며 트리인 부분 그래프, DFS나 BFS를 사용.

최소 비용 신장 트리(MST, Minimum Spanning Tree)
가중치를 가진 무방향 그래프에서 비용이 최소인 신장 트리
① Kruskal 알고리즘
각 단계에서 사이클을 형성하지 않으면서 비용이 최소인 간선을 선택한다.

② Prim 알고리즘
각 단계에서 사이클을 형성하지 않으면서 인접한 간선 중 비용이 최소인 간선을 선택한다.

4. 모든 쌍에 대한 최단 경로
방법1. 다익스트라 알고리즘을 모든 정점에 대하여 수행
방법2. Ford 알고리즘을 이용.
'Domain > 자료구조' 카테고리의 다른 글
| 4. 히프 트리(Heap Tree) (0) | 2020.03.12 |
|---|---|
| 5. 이진 탐색 트리(BST, Binary Searching Tree) (0) | 2020.03.12 |
| 7. 탐색 (0) | 2020.03.11 |
| 8. 정렬(Sort) (0) | 2020.03.11 |
| 9. Hashing(해싱) (0) | 2020.03.11 |


