지도 학습과 비지도 학습
머신러닝 알고리즘은 크게 지도 학습과 비지도 학습으로 나뉜다. 지도 학습에서는 데이터와 정답을 입력과 타깃이라고 부르고 이 둘을 합쳐 훈련 세트라고 한다. 그리고 입력으로 사용된 데이터의 길이, 무게와 같은 자료를 특성이라고 한다. 그리고 실제 평가에 사용하는 데이터를 테스트 세트라고 한다. 가장 간단한 방법은 전체 데이터 중 일부를 훈련 세트, 일부를 테스트 세트로 활용할 수 있다.
numpy와 scikitlearn을 활용하여 전체 데이터를 훈련/테스트 세트로 나누기
fish_length = [25.4, 26.3, 26.5, 29.0, 29.0, 29.7, 29.7, 30.0, 30.0, 30.7, 31.0, 31.0,
31.5, 32.0, 32.0, 32.0, 33.0, 33.0, 33.5, 33.5, 34.0, 34.0, 34.5, 35.0,
35.0, 35.0, 35.0, 36.0, 36.0, 37.0, 38.5, 38.5, 39.5, 41.0, 41.0, 9.8,
10.5, 10.6, 11.0, 11.2, 11.3, 11.8, 11.8, 12.0, 12.2, 12.4, 13.0, 14.3, 15.0]
fish_weight = [242.0, 290.0, 340.0, 363.0, 430.0, 450.0, 500.0, 390.0, 450.0, 500.0, 475.0, 500.0,
500.0, 340.0, 600.0, 600.0, 700.0, 700.0, 610.0, 650.0, 575.0, 685.0, 620.0, 680.0,
700.0, 725.0, 720.0, 714.0, 850.0, 1000.0, 920.0, 955.0, 925.0, 975.0, 950.0, 6.7,
7.5, 7.0, 9.7, 9.8, 8.7, 10.0, 9.9, 9.8, 12.2, 13.4, 12.2, 19.7, 19.9]
import numpy as np
#1열엔 fish_length, 2열엔 fish_weight가 존재하는 2차원 배열
fish_data = np.column_stack((fish_length, fish_weight))
# fish_target = [1]*35 + [0]*14
fish_target = np.concatenate((np.ones(35),np.zeros(14)))
"""
기존의 랜덤 배분 방법
np.random.seed(42) #책과 동일한 실습 결과를 얻기 위함. 랜덤 결과가 일정
index = np.arange(49) #0~49까지의 값을 갖는 배열 생성
np.random.shuffle(index) #배열 섞기
#인풋값의 35까지는 훈련 세트 35 이후는 테스트 세트로 랜덤하게 설정
# 훈련 세트 랜덤화
train_input = input_arr[index[:35]] #값이 랜덤한 인덱스 배열의 0~35까지 차례대로 추출하여 선택 0->0,1->7,2->8, ...
train_target = target_arr[index[:35]] #값이 랜덤한 인덱스 배열의 36~49까지 차례대로 추출하여 선택
# 테스트 세트 랜덤화
test_input = input_arr[index[35:]]
test_target = target_arr[index[35:]]
"""
# 사이킷런 활용 랜덤 배분
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(fish_data, fish_target, random_state=42)위처럼 데이터는 적절히 섞여야한다. 그렇지 않으면 한쪽만 편향되게 학습되는 샘플링 편향이 발생할 수 있다.
수상한 도미
수상한 도미 한마리가 존재한다. 분명 산점도 상에 근접한건 도미인데 결과로 빙어를 정답으로 출력한다.
# 수상한 도미 찾기
from sklearn.neighbors import KNeighborsClassifier
kn = KNeighborsClassifier()
kn = kn.fit(train_input,train_target) #훈련 세트로 훈련
kn.score(test_input,test_target) #테스트 세트로 결과 예측 결과:1.0
print(kn.predict([[25,150]]))
# 데이터와 수상한 도미 한마리 산점도
import matplotlib.pyplot as plt
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25,150, marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
distances, indexes = kn.kneighbors([[25,150]]) #n_neighbor=5라 기본값인 5개의 근접 이웃 거리, 인덱스 추출
plt.scatter(train_input[:,0], train_input[:,1])
plt.scatter(25,150, marker='^')
plt.scatter(train_input[indexes,0],train_input[indexes,1], marker='D')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
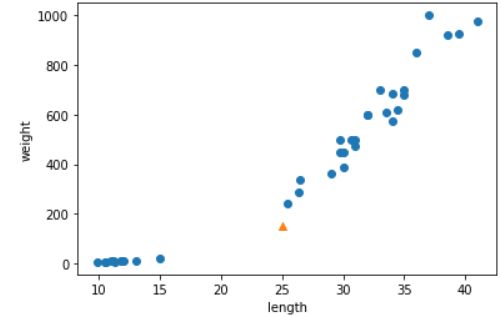

실제 근접한 값 5개를 찾은 결과 빙어가 더 많긴 하다. 왜 이런 결과가 나타난 것일까? 그 이유는 바로 length와 weight의 비중이 다르기 때문이다. y축으로 올라갈 수록 x축보다 실제 거리의 차이가 확연히 벌어진다. x축은 5단위이고 y축은 200단위여서 단순히 빙어가 가까워 보이는 것이다.
위와 같은 상황을 막기 위해서는 적절한 기준값이 필요하다. 이를 위해 필요한 작업이 데이터 전처리이다. 보통 이런 상황에서 널리 사용하는 전처리 방법은 표준점수(z점수)이다. 표준점수는 각 특성값이 0에서 표준편차의 몇 배 만큼 떨어져 있는지를 나타내 특성값의 크기와 상관없이 동일한 조건으로 비교가 가능하다.
mean = np.mean(train_input, axis=0)
std = np.std(train_input, axis=0)
train_scaled = (train_input - mean) / std #브로드 캐스팅: train_input의 모든 행에서 평균(meanm)값 만큼 빼준다.
sample = ([25,150]-mean)/std # 샘플도 표준점수화
다음은 실제 표준점수를 활용하여 산점도를 그리고 데이터를 예측한 결과이다.
plt.scatter(train_scaled[:,0], train_scaled[:,1])
plt.scatter(sample[0],sample[1], marker='^')
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
# 이제는 확실히 샘플이 도미에 가까워짐
test_scaled = (test_input - mean) / std #브로드 캐스팅: train_input의 모든 행에서 평균(meanm)값 만큼 빼준다.
kn.fit(train_scaled, train_target)
kn.score(test_scaled, test_target)
print(kn.predict([sample])) #예측된 결과는 성공적으로 도미로 출력되었다.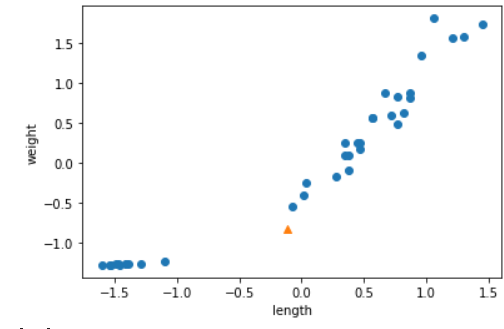
스케일이 모두 같아졌고, 확실히 해당하는 샘플은 도미로 판정이 났다.
'AI: ML,DL' 카테고리의 다른 글
| [인공지능] 확률적 경사 하강법 (0) | 2021.03.15 |
|---|---|
| [인공지능] 로지스틱 회귀 (0) | 2021.03.14 |
| [인공지능] 특성 공학과 규제(다중 회귀, 릿지, 라쏘) (0) | 2021.03.13 |
| [인공지능] 회귀: k-최근접 이웃 회귀 (0) | 2021.03.13 |
| [인공지능] 머신러닝, 딥러닝 개요 (0) | 2021.03.12 |



