회귀
지도 학습 알고리즘은 크게 회귀와 분류로 나뉜다. 분류는 이전 포스팅에서 다루었다. 샘플을 몇 개의 클래스 중 하나로 분류하는 문제이다. 회귀는 클래스로 분류하는 것이 아닌 어떤 숫자를 예측하는 문제이다. 예를 들어, 내년 경제 성장률, 배달 도착 시간 등의 예측이 존재한다.
k-최근접 이웃 회귀
이전의 k-최근접 이웃 분류의 경우 알고리즘이 간단하다. 데이터 근처에 많은 샘플 존재하는 클래스를 택하면 된다. k-최근접 이웃 회귀의 경우도 비슷하다. 주변 데이터를 선택하고 그 데이터 값을 평균을 내어 값을 예측한다.
예제: 농어의 길이로 무게를 예측하기
농어의 길이가 특성이되고, 무게는 타깃이 된다.
길이와 무게 데이터로 산점도 그리기
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
import matplotlib.pyplot as plt
plt.scatter(perch_length, perch_weight)
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
k-최근접 이웃 회귀 알고리즘 사용
# 훈련세트와 테스트세트로 나눔
from sklearn.model_selection import train_test_split
train_input, test_input,train_target, test_target = train_test_split(perch_length,perch_weight,random_state=42)
#사이킷런 모델은 2차원 배열 형태여야 함.
#-1:모든 원소, 전체 개수를 몰라도 됨
train_input = train_input.reshape(-1,1)
test_input = test_input.reshape(-1,1)
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input,train_target) #훈련
print(knr.score(test_input,test_target)) #결정계수
#--> 0.9928094061010639위에서 결정계수(R^)란 예측이 결과(타깃)에 얼마나 가까운지를 나타내는 계수이다. 회귀에서 숫자를 정확히 맞히는 것은 사실상 불가능하기 때문에 확률로 표시한다.
하지만 이 예측이 직감적으로 얼만큼 차이나는지는 눈에 보이지 않는다. 아래와 같이 코딩하여 차이를 알 수 있다.
from sklearn.metrics import mean_absolute_error
test_prediction = knr.predict(test_input) #훈련 세트에 대한 예측
mae = mean_absolute_error(test_target, test_prediction) #실제 결과 모델의 에측의 평균 차이
print(mae)
#--> 19.157142857142862결과로 평균 19g 정도 예측이 타깃과 다르다는 것을 알 수 있다.
과대적합과 과소적합
앞에서 훈련한 모델을 통해 시범삼아 훈련에 사용된 훈련 세트에 대해 R^을 확인해본 결과이다.
print(knr.score(train_input,train_target))
#--> 0.9698823289099255훈련 세트로 훈련한 모델은 훈련 세트에 잘 맞는 모델이 생성된다. 따라서, 훈련세트의 결정계수가 더 높게 나와야된다.
이 관계 중 만약, 훈련 세트에서 점수가 굉장히 좋았는데 테스트 세트에서는 매우 나쁘다면 모델이 훈련 세트에 과대 적합되었다고 말한다 (훈련 세트에만 잘 맞는 모델). 반대로 훈련 세트보다 테스트 세트의 점수가 높거나 훈련 세트, 테스트 세트 점수가 모두 낮은 경우를 과소 적합이라고 얘기한다 (적절히 훈련되지 않은 경우, 훈련 세트/테스트 세트의 크기가 작아서 발생하는 문제).
따라서 위의 문제는 과소 적합이라고 볼 수 있다. 테스트 세트의 경우 약 0.99, 훈련 세트의 경우 약 0.96이 나왔기 때문이다. 과소 적합을 해결하기 위해서는 모델을 좀 더 복잡하게 만들면 된다. 즉, 훈련 세트에 더 적합하게 만들면 된다. k-최근접 이웃 회귀에서는 단순히 판단하는 이웃의 수를 줄이면 아주 일부만 보고 판단하기 때문에 훈련 세트에 더 유사해진다. (반대로 이웃의 수를 늘리면 데이터 전반에 있는 일반적인 패턴에 대한 판단을 한다.)
knr.n_neighbors=3
knr.fit(train_input, train_target)
print(knr.score(train_input,train_target))
print(knr.score(test_input,test_target))
훈련 세트: 0.9804899950518966
테스트 세트: 0.974645996398761이웃을 줄여 훈련 세트와 테스트 세트의 결정계수가 거의 유사해졌다.
선형 회귀
위 모델에는 문제점이 존재한다. 만약 길이가 매우 긴 50cm 짜리 농어의 무게를 예측하면 얼마가 나올까?
print(knr.predict([[50]]))
결과: [1033.33333333]1033g으로 측정됐는데 실제 농어의 무게는 훨씬 많이 나간다고 한다. 왜 이런 결과가 나타났는지 산점도를 통해 확인해보자.
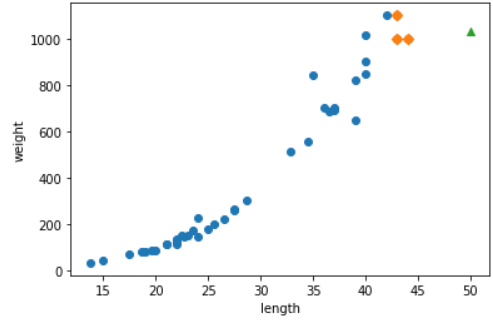
산점도를 통해 확인해보면 길이가 증가할수록 무게가 증가해야 정상이다. 하지만 50cm 농어에 가까운 샘플은 45cm 근방의 농어만 존재하기 때문에 이 샘플들의 무게를 평균하여 나타난 결과이다. 따라서, 100cm 농어를 예측해도 무게는 1033g이 나올 것이다.
이를 극복하기 위해 나온 알고리즘이 선형 회귀 알고리즘이다. 데이터의 특성을 잘 나타내는 직선을 찾는 알고리즘이다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target)
print(lr.predict([[50]]))
결과: [1241.83860323]선형 회귀 알고리즘을 사용할 경우 50cm 무게 농어를 무겁게 평가했다.
앞서 말한듯 선형 회귀는 직선을 찾는다. 직선을 그리기 위해서는 기울기와 y의 절편만 있으면 그릴 수 있다. 이 값은 아래와 같이 찾을 수 있다. 이를 활용하여 실제 그래프를 그린다.
# 기울기, 절편
print(lr.coef_,lr.intercept_)
#y = lr.coef_*x + lr.intercept_
#15~50까지 1차 방정식 그래프를 그린다.
#-> (15,[lr.coef_*15 + lr.intercept_])점과 (50,[lr.coef_*50 + lr.intercept_])점을 잇기
plt.plot([15,50], [lr.coef_*15 + lr.intercept_, lr.coef_*50 + lr.intercept_])
plt.scatter(train_input, train_target)
plt.scatter(50,1241.8, marker='^')
plt.xlabel("length")
plt.ylabel("weight")
plt.show()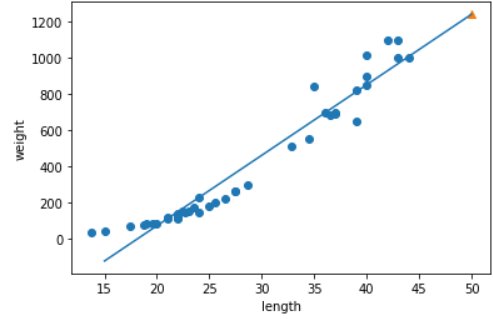
위 모델을 결정계수로 실제 평가해보자.
print(lr.score(train_input, train_target))
print(lr.score(test_input, test_target))
# 0.9398463339976039
# 0.8247503123313558단순히 둘 차이만 보면 훈련세트에 과대적합 되었다고 볼 수 있지만, 사실 둘 다 점수가 낮아 과소적합이다. 이 문제점은 그래프 좌하단에서 찾을 수 있다. 농어 무게의 산점도를 보면 사실 직선이라기 보다는 곡선이다. 따라서, 2차 방정식이 더 예측에 적합하다.
2차 방정식으로 만들기 위해 길이를 제곱한 항을 훈련 세트에 추가해야 한다.
#기존 열에 제곱 열 추가
train_poly = np.column_stack((train_input**2, train_input))
test_poly = np.column_stack((test_input**2, test_input))
lr.fit(train_poly, train_target)
#50cm 농어 에측이 제곱한 값을 첫번째 열로 추가(위에서 넣기 때문에 식이 같아야 함)
lr.predict([[50**2,50]])
결과: array([1573.98423528])이 모델에서는 더 높은 값을 에측했다. 해당 모델에서는 아래와 같은 그래프를 학습했다.
print(lr.coef_,lr.intercept_)
[ 1.01433211 -21.55792498] 116.05021078278276Y = 1.01X^ - 21.6X + 116.05
위와 같은 방정식을 수학에서는 다항식이라고 불렀다. 이를 활용한 선형 회귀를 다항 회귀라고 한다.
이제 마지막으로 위 모델의 산점도를 그리고 모델을 평가한다.
# 15~50까지 매우 짧은 직선을 1씩 끊어서 그려 곡선을 표현
point = np.arange(15,50)
plt.scatter(train_input,train_target)
plt.plot(point, 1.01*point**2-21.6*point + 116.05)
plt.scatter(50,1573, marker='^')
plt.xlabel("length")
plt.ylabel("weight")
plt.show()
print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))
#결과:0.9706807451768623
#결과:0.9775935108325122
실제 농어 데이터와 모델의 예측이 매우 유사해졌다. 그리고 훈련세트와 테스트세트에 대한 결정계수도 매우 높아졌다. 하지만 아직 테스트 점수가 약간 높아 과소적합이 남아있다.
'AI: ML,DL' 카테고리의 다른 글
| [인공지능] 확률적 경사 하강법 (0) | 2021.03.15 |
|---|---|
| [인공지능] 로지스틱 회귀 (0) | 2021.03.14 |
| [인공지능] 특성 공학과 규제(다중 회귀, 릿지, 라쏘) (0) | 2021.03.13 |
| [인공지능] 데이터: 훈련 세트와 테스트 세트, 데이터 전처리 (0) | 2021.03.12 |
| [인공지능] 머신러닝, 딥러닝 개요 (0) | 2021.03.12 |



